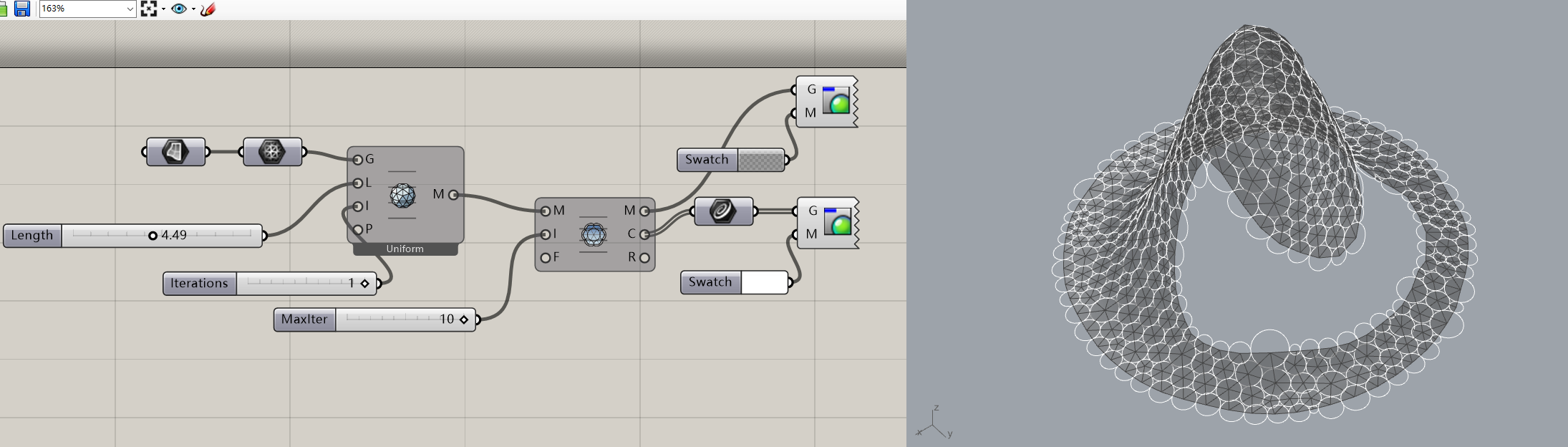
### **CPMesh (Circle Packing Mesh)** * * * * * **Description**： CP mesh (Circle Packing Mesh) developed to rationalize freeform surfaces in architecture and design originally, a CP mesh is a triangle mesh whose incircles form a packing. A CP mesh is a triangle mesh whose incircles (orange) form a packing. Then spheres (blue), which are centered at mesh vertices and are orthogonal to the incircles of neighboring triangles form a packing, too. Centers and axes of incircles defifine a hexagonal support structure with [**Torsion-Free Nodes**]([https://discourse.mcneel.com/t/about-pq-mesh-conjugate-curvature-network/83476/5](https://discourse.mcneel.com/t/about-pq-mesh-conjugate-curvature-network/83476/5)) (red, see Figure 1). :-:  Figure 1. Graph of CP Mesh. Adapted from 'Packing circles and spheres on surfaces'. "CP meshes have some useful properties which are quite relevant to various algorithms and applications. One of these properties is that they form an ideal primal/dual structure which guarantees orthogonality, non-intersection and convexity. This is important in case we are using discrete differential geometry operators: Orthogonality ensures good numerical qualities of the Laplacian and furthermore it ensures that we can safely compute primal values based on the dual values and dual values based on primal values respectively. Another important property of a CP mesh is that if we extrude the edges of the dual polygon we get a [**Torsion Free Structure**]([https://discourse.mcneel.com/t/about-pq-mesh-conjugate-curvature-network/83476/5](https://discourse.mcneel.com/t/about-pq-mesh-conjugate-curvature-network/83476/5)). In other words, its physical realization could be build out of beams which intersect in a common axis passing through the incircles center. And last but not least, CP meshes can be used to approximate circle packings on a surface. This could be done by either fitting a circle into each vertex gap between the incircle packing or by using the contact points of the sphere packing. Both methods generally produce a fairly good packing. A real circle packing however, is not possible on an arbitrary surface." --: ——Houdini Gubbins If you wanna learn more about CP mesh, please read references as follows or visit [**Houdini Gubbins**]([https://houdinigubbins.wordpress.com/2017/06/07/cp-meshes/](https://houdinigubbins.wordpress.com/2017/06/07/cp-meshes/)) **Input**： * Mesh: The mesh model to be optimized. * Iteration: A maximum number of remesh iterations. * Fixed: If ture, boundaries will be fixed in the process of optimization. Or fix the original mesh. **Output**： * Mesh: Return the optimized CP Mesh. * Circles: Return a Circle Packing from Ball Packing. * Radii: Return all radii of the Circle Packing. :-:  :-:  **References** \[1\] Pottmann H, Eigensatz M, Vaxman A, Wallner J. Architectural geometry. Computers & graphics. 2015 Apr 1;47:145-64.