# 姿态解算
## 1.四个坐标系
### 1.1.世界坐标系
是客观三维世界的绝对坐标系,对于这个坐标系的定义是任意的,我们可以人为的规定,世界坐标系的原点以及各坐标轴的正方向,但在我们后续的解算中,为了获得相机与装甲板中心之间准确的位置信息,我们往往选取装甲板中心为坐标原点。
|  |
| :---------------------------------: |
| *世界坐标系的建立* |
### 1.2.相机坐标系
也为右手坐标系,以光心为原点,你可以伸出右手,让大拇指朝前(z轴)、食指朝右(x轴)、中指朝下(y轴),此时此刻,想象你的右手就是一部相机,而大拇指就是从相机中延伸出的镜头,相机就这样镜头朝前平放着,相机运动的同时也带动着坐标系一起运动。相机坐标系用来描述三维世界中的物体与相机之间的位置关系。
### 1.3.图像坐标系
以图像平面的中心为坐标原点,X轴和Y轴分别平行于图像平面的两条垂直边,用( x , y )表示其坐标值。图像坐标系是用物理单位(例如毫米)表示像素在图像中的位置。
### 1.4.像素坐标系
以图像平面的左上角顶点为原点,X 轴和Y 轴分别平行于图像坐标系的 X 轴和Y 轴,用(u , v )表示其坐标值。数码相机采集的图像首先是形成标准电信号的形式,然后再通过模数转换变换为数字图像。每幅图像的存储形式是M × N的数组,M 行 N 列的图像中的每一个元素的数值代表的是图像点的灰度。这样的每个元素叫像素,像素坐标系就是以像素为单位的图像坐标系。
## 2.坐标系之间的变换
### 2.1.图像坐标系与像素坐标系的变换
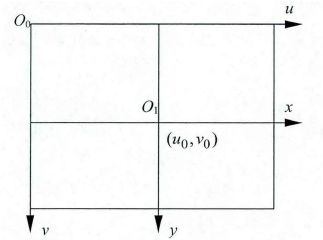
通过相机拍摄,我们可以直接获得的就是像素坐标,而后序计算所使用的却是图像坐标,所以第一步就是要进行二者之间的转换,二者关系如下图所示:
../image/
|  |
| :--------------------------------------------------------------------------------------------: |
| *坐标系关系* |
图像坐标与像素坐标的转换涉及到平移以及单位的转换,我们设dx,dy分别为每个像素在图像平面x和y方向的物理尺寸,可以得到如下转换公式:
这里的变换关系
```[tex]
u = \frac{x}{dx} + u_0 \ , \ v = \frac{y}{dy} + v_0
```
(`$ dx $`为每个像素在横轴x上的尺寸,`$ dy $`为每个像素在纵轴y上的尺寸)
### 2.2.像素坐标系与相机坐标系的变换
我们可以使用相机坐标系与世界坐标系描述三维空间物体的位置,但是我们现在只有像素坐标系,因此将像素坐标系转为相机坐标系是必要的,四个坐标系的关系如下图所示:(下标C为相机坐标,下标W为世界坐标,另外为了方便理解,我在图上画出了必要的标注)
|  |
| :-----------------------------: |
| *坐标系关系图* |
由三角形的相似,我们可以得到如下的几何关系:
```[tex]
\frac{f}{Z_c} = \frac{x}{X_c} => f\frac{X_c}{Z_c} \\ \ \\
\frac{f}{Z_c} = \frac{y}{Y_c} => f\frac{Y_c}{Z_c}
```
由2.1我们得到的两个式子,联立并且写成矩阵连乘形式如下:(这里涉及到两个问题,为什么写成矩阵连乘怎么写成矩阵连乘以及齐次坐标,不过多赘述,如果不清楚的新队员可以自行学习),这样我们就得到了像素坐标系与相机坐标系的变换关系,这是我们想看到的,接下来,如果有相机坐标系与世界坐标系的变换关系,那么我们就通过手上的像素坐标成功的与世界坐标建立了联系,离解算成功就不远了。
```[tex]
Z_c
\begin{bmatrix}
u \\
v \\
1
\end{bmatrix} =
\begin{bmatrix}
\frac{1}{dx} & 0 & u_0 \\
0 & \frac{1}{dy} & v_0 \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
f & 0 & 0 & 0 \\
0 & f & 0 & 0 \\
0 & 0 & 1 & 0
\end{bmatrix}
\begin{bmatrix}
X_{c} \\
Y_{c} \\
Z_{c} \\
1
\end{bmatrix}
```
### 2.3相机坐标系与世界坐标系的变换
推导过程不再写出,感兴趣的可以自己去了解,能对这个问题领悟的更深入。变换关系如下:
```[tex]
\begin{bmatrix}
X_c \\
Y_c \\
Z_c \\
1
\end{bmatrix} =
\begin{bmatrix}
R & T \\
0 & 1
\end{bmatrix}
\begin{bmatrix}
X_{w} \\
Y_{w} \\
Z_{w} \\
1
\end{bmatrix}
```
```[tex]
\begin{bmatrix}
X_c \\
Y_c \\
Z_c \\
1
\end{bmatrix} =
\begin{bmatrix}
r_{11} & r_{12} & r_{13} & t_x \\
r_{21} & r_{22} & r_{23} & t_y \\
r_{31} & r_{32} & r_{33} & t_z \\
0 & 0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
X_{w} \\
Y_{w} \\
Z_{w} \\
1
\end{bmatrix}
```
请注意,等号左边的第一个矩阵是一个分块阵,R是相机坐标系与世界坐标系之间的旋转矩阵,是一个3×3的矩阵,t是相机坐标系与世界坐标系之间的平移矩阵,代表着从各个轴平移多少的数量才能从相机坐标系到世界坐标系,是一个3×1的矩阵,请记住,这两个矩阵尤其是平移矩阵对我们后面的解算非常重要。
### 2.4最后联立
我们将上面所有的过程凝练,将部分矩阵相乘起来,最后得到的像素坐标与世界坐标的变换关系如下:
```[tex]
Z_c
\begin{bmatrix}
u \\
v \\
1
\end{bmatrix} =
\begin{bmatrix}
a_x & 0 & u_0 & 0 \\
0 & a_y & v_0 & 0 \\
0 & 0 & 1 & 0
\end{bmatrix}
\begin{bmatrix}
r_{11} & r_{12} & r_{13} & t_x \\
r_{21} & r_{22} & r_{23} & t_y \\
r_{31} & r_{32} & r_{33} & t_z \\
0 & 0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
X_{w} \\
Y_{w} \\
Z_{w} \\
1
\end{bmatrix}
```
其中`$ a_x = \frac{f}{dx}, a_y = \frac{f}{dy} $`。
通过观察我们可以发现,等号右边的第一个矩阵是由相机内部结构决定的,这也是我们将两个矩阵合并成这一个矩阵的原因,第二个矩阵是由相机坐标系与世界坐标系的相对位置决定的,不要忘记我们结算的最终目的:获取装甲板相对于云台的位置信息,所以这个矩阵对我们尤其关键!我们再观察一下这个结构,除了等号右边第二个矩阵,其他的都是已知的,我们的后续的目的就是根据已知的条件求出这个矩阵里的R和t。
## 3.解算获取相对欧拉角
### 3.1 有关 `solvePnP() `
在2.4中,我们提到了我们的目的是获取R和t,opencv官方给出了一个解决办法。
```c++
bool cv::solvePnP ( InputArray objectPoints,
InputArray imagePoints,
InputArray cameraMatrix,
InputArray distCoeffs,
OutputArray rvec,
OutputArray tvec,
bool useExtrinsicGuess = false,
int flags = SOLVEPNP_ITERATIVE
)
/**
@brief Finds an object pose from 3D-2D point correspondences.
简介 从3D-2D点对应中查找对象姿势。
This function returns the rotation and the translation vectors that transform a 3D point expressed in the object coordinate frame to the camera coordinate frame, using different methods:
此函数返回旋转和平移向量,这些向量使用不同的方法将对象坐标帧中表示的三维点转换为摄影机坐标帧:
- P3P methods (@ref SOLVEPNP_P3P, @ref SOLVEPNP_AP3P): need 4 input points to return a unique solution.
- P3P方法(@ref SOLVEPNP_P3P,@ref SOLVEPNP_AP3P):需要4个输入点才能返回唯一的解决方案。
- @ref SOLVEPNP_IPPE Input points must be >= 4 and object points must be coplanar.
- @ref SOLVEPNP_IPPE输入点必须大于等于4且对象点必须共面。
- @ref SOLVEPNP_IPPE_SQUARE Special case suitable for marker pose estimation.
Number of input points must be 4. Object points must be defined in the following order:
-@ref SOLVEPNP_IPPE_SQUARE适用于标记姿势估计的特殊情况。输入点的数量必须为4。必须按以下顺序定义对象点:
- point 0: [-squareLength / 2, squareLength / 2, 0]
- point 1: [ squareLength / 2, squareLength / 2, 0]
- point 2: [ squareLength / 2, -squareLength / 2, 0]
- point 3: [-squareLength / 2, -squareLength / 2, 0]
- for all the other flags, number of input points must be >= 4 and object points can be in any configuration.
对于所有其他标志,输入点的数量必须大于等于4,并且对象点可以是任何配置。
@param objectPoints Array of object points in the object coordinate space, Nx3 1-channel or 1xN/Nx1 3-channel, where N is the number of points. vector<Point3dcan be also passed here.
@param imagePoints Array of corresponding image points, Nx2 1-channel or 1xN/Nx1 2-channel, where N is the number of points. vector<Point2dcan be also passed here.
@param cameraMatrix Input camera intrinsic matrix cameramatrix .
@param distCoeffs Input vector of distortion coefficients. If the vector is NULL/empty, the zero distortion coefficients are assumed.
@param rvec Output rotation vector (see @ref Rodrigues ) that, together with tvec, brings points from the model coordinate system to the camera coordinate system.
@param tvec Output translation vector.
@param useExtrinsicGuess Parameter used for #SOLVEPNP_ITERATIVE. If true (1), the function uses the provided rvec and tvec values as initial approximations of the rotation and translation vectors, respectively, and further optimizes them.
@param flags Method for solving a PnP problem
The function estimates the object pose given a set of object points, their corresponding image projections, as well as the camera intrinsic matrix and the distortion coefficients, see the figure below (more precisely, the X-axis of the camera frame is pointing to the right, the Y-axis downward and the Z-axis forward).
该函数估计给定一组对象点的对象姿势、其对应的图像投影以及相机固有矩阵和失真系数,请参见下图(更准确地说,相机帧的X轴指向右侧,Y轴向下,Z轴向前)。
*/
```
分别解释一下这些参数
```c++
// objectPoints : 传入参数,自定义的世界坐标,在解算装甲板姿态时传入的是在"1.1"世界坐标系定义下装甲板的四个角点坐标。
// imagePoints : 传入参数,识别到的装甲板的四个角点的像素坐标。
// cameraMatrix : 传入参数,相机的内参矩阵,包含相机的焦距以及每个像素在相平面的物理尺寸的元素,由相机标定获得。
// distCoeffs : 传入参数,畸变系数矩阵,描述相机畸变情况,由相机标定获得。
// rvec : 输出参数,相机坐标系与世界坐标系之间的旋转矩阵
// tvec : 输出参数,相机坐标系与世界坐标系之间的平移矩阵
// flags : 解算类型,默认即可
```
### 3.2几何关系求欧拉角(第一档位)
当相机与装甲板距离小于五米时,我们通过精确的几何关系获取欧拉角中的pitch以及yaw,如下图所示:
|  |
| :---------------------------------: |
| *几何关系求欧拉角* |
在3.1中算出的平移矩阵t,此时在这里就要使用,我们可以简单的认为,平移矩阵的元素和相机坐标一一对应,即x_pos(平移矩阵里第一个元素) == Xc,依次类推,因此可以取出运算。
```c++
double x_pos = armor.GetTransVec().at<double>(0, 0);
double y_pos = armor.GetTransVec().at<double>(1, 0);
double z_pos = armor.GetTransVec().at<double>(2, 0);
```
得到以下关系(要注意正负方向的问题)
```[tex]
\tan(pitch) = \frac{-Y_c}{X_c^2+Z_c^2} \\ \ \\
\tan(yaw) = \frac{X_c}{Z_c}
```
反三角运算即可得到pitch以及yaw
```c++
aiming_eulr.pitch = -atan(y_pos / sqrt(x_pos * x_pos + z_pos * z_pos));
aiming_eulr.yaw = atan(x_pos / z_pos);
```
### 3.3小孔成像原理求欧拉角(第二档位)
当相机与装甲板距离小于五米时,一些误差可以忽略,我们使用基于小孔成像原理的解算,回顾2.2中我们所得到的像素坐标与相机坐标的变换关系,将矩阵形式写成方程组形式,我们可以得到如下的结果:
```[tex]
\begin{matrix}
\begin{cases}
u = a_x \cdot \frac{X_c}{Z_c} + u_0 & (a_x = \frac{f}{dx})\\
v = a_y \cdot \frac{Y_c}{Z_c} + v_0 & (a_y = \frac{f}{dy})
\end{cases}
\end{matrix}
\\ \ \\
\tan(pitch) = \frac{-Y_c}{X_c^2+Z_c^2} = -\frac{u - u_0}{a_x} \\ \ \\
\tan(yaw) = \frac{X_c}{Z_c} = \frac{v - v_0}{a_y}
```
反三角运算即可得到pitch以及yaw
```c++
aiming_eulr.pitch = -atan((out.front().y - v0) / ay);
aiming_eulr.yaw = atan((out.front().x - u0) / ax);
```
# 重力补偿
## 为什么补偿
解算出欧拉角后,经过通信以及电控的控制,会使得枪口指向装甲板中心,但是由于重力的存在,子弹难免出现下坠以致打击不精确,依次需要给枪口一定的抬头补偿,这里主要处理的是pitch角。
## 怎么补偿
我们只研究枪口以及装甲板之间的竖直切平面,画出示意图并且列出方程组,解方程组即可:
|  |
| :----------------------------: |
| *补偿示意图* |
