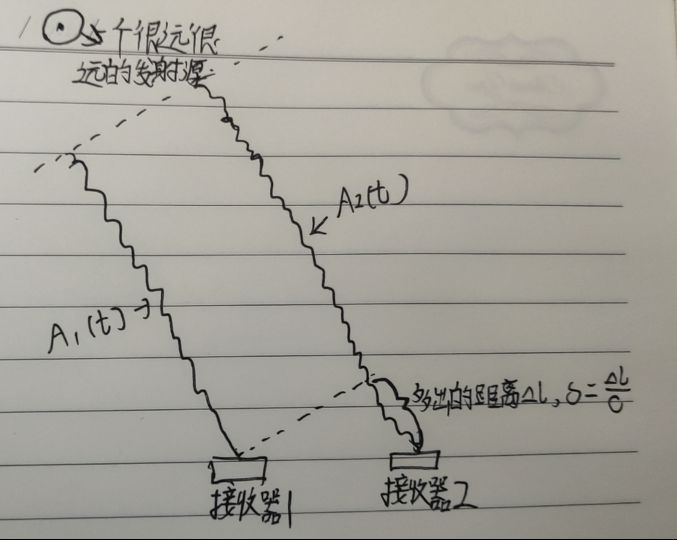
**总体目标：制作一种模块化的、买得起的相干多通道软件定义无线电（software-defined radio,SDR）接收机。** ### 电-视棒 下图是常见的RTL.SDR接收机，也叫做电-视棒。一端是USB口，可以连接电脑；另一端是SMA接口，可以接馈线（导线）；然后馈线又和天线相接，天线可以接收电磁波信号。  ### 相干和非相干  *图1.两个接收器从一个发射源接收信号，可以大致认为电磁波的表达式和电压`$ A_1(t),A_2(t) $`的形式类似。同时这个发射源足够远，可认为这个发射源发出的光是平行光。实际情况是用天线接收电磁波的，然后输出到接收器，图中省略了天线。* \ 一个移动源发出电磁波信号被两个接收机捕获，捕获的余弦电压信号形式分别为`$ A_1(t)=Acos(\omega t),A_2(t)=Acos(\omega t-\delta) $`，其中`$ A_1,A_2 $`的振幅都是`$ A $`;`$ A_2(t) $` 中的`$ -\delta $`项是由于从源发出的电磁波信号到接收器2比接收器1多出了一段距离，这段距离导致`$ A_2(t) $`的相位滞后了`$ \delta $`。由于源的移动会导致`$ \delta $`的变化，所以`$ \delta $`是个变量。  接收器所测值显然都是平均功率，即电压信号`$ A(t) $`平方之后再取足够的时间平均，记成`$ \lang A(t)^2 \rang $`，其中符号`$ \lang\rang $`表示对`$ A(t)^2 $`取时间平均。由欧姆定理知`$ P=V^2/R $`，但实际中我们会忽略常数`$ R $`，用`$ P=V^2 $`直接表征功率，所以用上述`$ \lang A(t)^2 \rang $`表示测得的平均功率。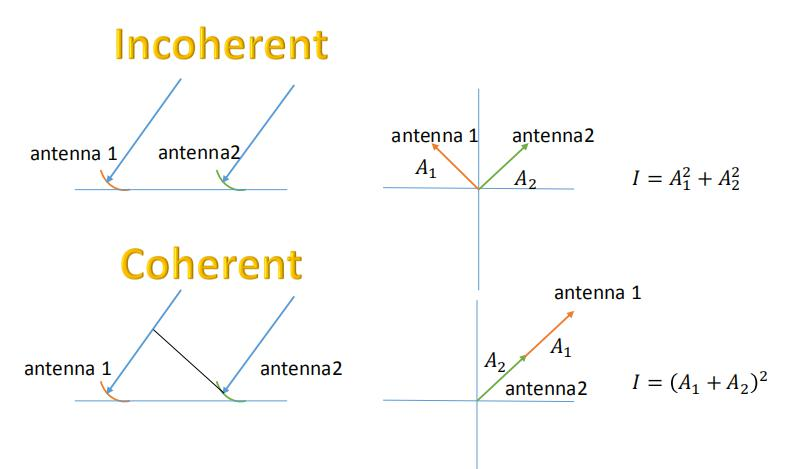 两个接收器接收到平均功率直接相加得到总功率，即`$ P_{非相干}=\lang A_1(t)^2 \rang+\lang A_2(t)^2 \rang $`，这种方法叫做非相干相加，因为不需要考虑`$ V_1,V_2 $`之间的相位差`$ \delta $`。 而如果在接收机内部便考虑相位`$ \delta $`，在接收器2中安装电子线路抵消掉`$ A_2(t) $`中的`$ \delta $`，使得`$ A_2=Acos(\omega t) $`，则我们可以直接令`$ A1+A2 $`，然后平方之后再取平均，即`$ P_{相干}=\lang (A1+A2)^2 \rang $`。 计算后可知，`$ P_{相干} / P_{非相干}=\sqrt{2} $`，即相干方法求功率比非相干方法求功率更好。 或许有人会疑惑，为什么不能把`$ A_1,A_2 $`直接相加，然后平方再求平均？因为`$ A_1,A_2 $`的相位差`$ \delta $`一直在变动，如果直接相加然后平方求平均，得到的平均值是0。对于相干这个词汇的理解可以百度[相干光](https://baike.baidu.com/item/%E7%9B%B8%E5%B9%B2%E5%85%89)。 在这里我没有考虑其他噪声项，不过即使考虑了，往往也不会改变结论。同时实际情况往往更为复杂，比如说不止两个接收器，还要要考虑其他一些因素的影响。 **我们所要做的就是在接收机内部实现类似的相干求功率，细节很多，我也不太了解，就不介绍了。** ### 差分联合阵列（Difference co-array） 所谓的联合阵列，就是利用了基线长度的不同，来进行傅里叶变换的叠加，从而得到源的形状。 稀疏阵列（sparse array）通常是通过由阵列单元之和或差模拟出虚拟联合阵列来实现的。差分联合阵列适用于被动传感设备，而相加联合阵列适用于主动传感设备。在大多数情况下，阵列单元之间的物理距离是半波长`$ \lambda/2 $`，此后阵列将以这个距离的整数d倍来描述。考虑一个有着`$ N $`个等间距分布的连续线性阵列，有着`$ L=N-1 $`个孔径。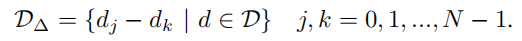让阵列单位的距离显得规范化，令`$ D=\{0,1,...,N-1\} $`，`$ |D|=N $`，那么差分联合阵列`$ D_{\Delta} $`  随着N的增加，式子中的冗余也增加，即上面的`$ d_j-d_k $`产生多个相同的差。一个`$ N\ge 3 $`的完全填充线性阵列总是有冗余的联合阵列。