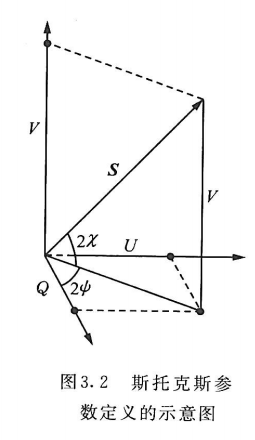
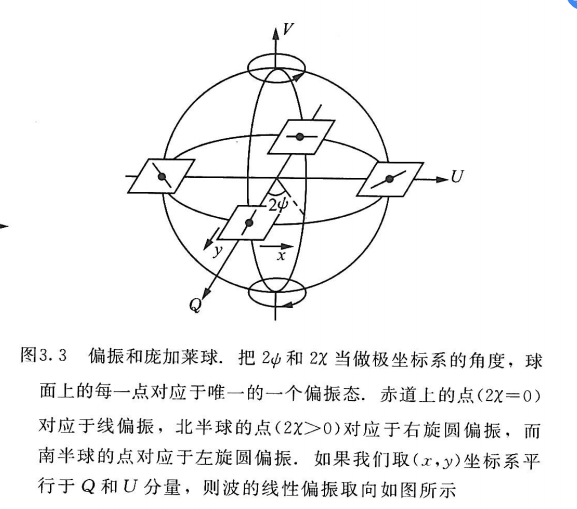
前面的结果表明，需要3个独立参量来描述一个单色矢量波的偏振状态，因此引入了几套参数： （1）两个正交线性偏振波的振幅`$ E_1,E_2 $`和相对相位`$ \delta $` （2）一个左旋圆偏振波和一个右旋圆偏振波的振幅`$ E_r,E_l $`和相对相位`$ \delta $` （3）偏振椭圆的长轴和短轴`$ E_a,E_b $`以及位置角`$ \psi $` 庞加莱（1892）引入了另一套方法，使得矢量波的不同的偏振状态很容易可视化。如果我们把式（3.19）的角度`$ 2\psi $`和式（3.21）的角度`$ 2\chi $`解释为一个半径为式（3.15）的`$ S_0 $`的球的经度和维度，那么在偏振状态和球上的点之间就有一一对应的关系（图3.2）：赤道代表线偏振，北极对应于右旋圆偏振，南极对应于左旋圆偏振（图3.3）。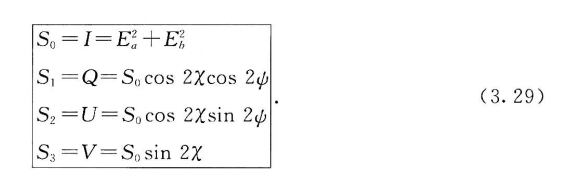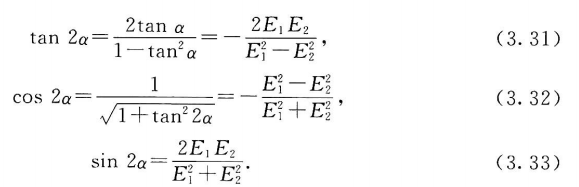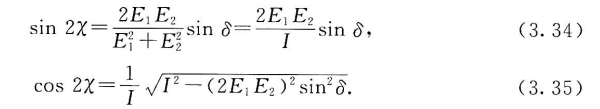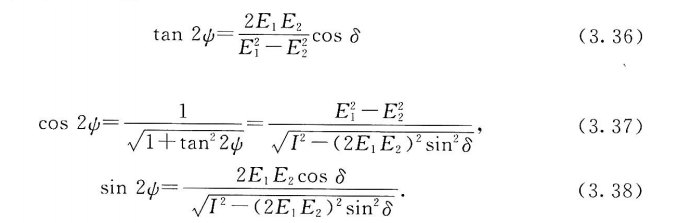   在庞加莱球和斯托克斯参数（1852）之间由一种自然的关联，即斯托克斯参数就是庞加莱球上的点在直角坐标系的对应坐标  这4个参数中只有3个是独立的，因为根据庞加莱球的建立有  斯托克斯参数也可以直接用偏振椭圆的参数式（3.4）表示，我们先从式（3.18）推导出  然后利用式（3.33）和式（3.15），从式（3.21）得到  从而式（3.19）和式（3.31）有  把式（3.34）、式（3.35）和式（3.37）、式（3.38）代入式（3.29），我们得到了期望的结果  这些方程把斯托克斯参数表示为可以直接观测的量。几个特殊的例子可以说明其原则。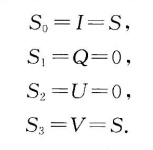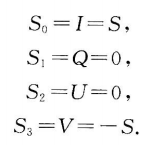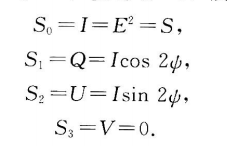 （1）右旋圆偏振波：`$ E_1=E_2 $`，而且`$ \delta=\pi/2 $`，所以  （2）左旋偏振波：  （3）线偏振波：`$ E_b=E,E_a=0 $`，使得`$ \chi=0 $`，所以  最后，应该注意到，到目前为止，我们隐含了（虽然没有明确阐述）“一个严格的单色波总是片真的”，没有非偏振的单色波，如果记得对于一个单色平面谐波，`$ E_1,E_2, \delta_1\delta_2 $`总是常数，这就是显而易见的。当转向准单色（`$ \omega $`限制在一个小而有限的带宽内）辐射时，情况就不一样了：这种类型的辐射可以时非偏振的或者部分偏振的。为了分析准单色波，必须用一种简便的方式来描述这种辐射，这就是下一节的任务。