## 8.2 密码学的原则 密码学技术使得发送方可以伪装数据，使入侵者不能从截取到的数据中获得任何信息，并且接受方必须能够从伪装的数据中恢复出初始数据。 * 报文的最初形式被称为明文（Plaintext，Cleartext）。 * 通过加密算法（Encryption Algorithm）加密明文。 * 生成的加密报文称为密文（Ciphertext），密钥（Key）为一串数字或字符，作为加密/解密算法的输入。 * 接受方通过解密算法（Decryption Algorithm）解密密文，以获得明文。 两种加密系统： * 对称密钥系统（Symmetric Key System）：加密和解密用的密钥相同，并且私密。 * 公开密钥系统（Public Key System）：使用一对密钥，其中一个密钥为公开，另一个密钥只有发送方或者接受方持有。 ### 8.2.1 对称密钥密码体系 **凯撒密码（Caesar Cipher）**：将明文报文中的每个字母用字母表中改字母后第k个字母进行替换，仅有25种可能。 **单码代替密码（Monoalphabetic）**：凯撒密码的改进，使用字母表中的一个字母替换该字母表中的另一个字母，有26！种可能，但是通过词组、频率等因素可以减少破译成本。 **多码代替密码（Polyalphabetic Encryption）**：对单码代替密码的改进，基本思想为使用多个单码代替密码，因此在明文中不同位置的同一字母可能一不同形式编码。 入侵者掌握信息程度： * 唯密文攻击（Ciphertext-only Attack）：入侵者只获得密文。 * 已知明文攻击（Known-plaintext Attack）：入侵者获取密文并了解密文中少量信息。 * 选择明文攻击（Chosen-plaintext Attack）：入侵者能够选择某一明文并得到该明文对应的密文形式。 对称加密有两种宽泛类型：流密码（Stream Ciphers）和块密码（Block Ciphers） #### 块密码 需要被加密的明文被处理为K比特的块，每个块被独立加密。但如果K=64，发送方和接收方需维护一张2的64次方的映射表，显然不能实现。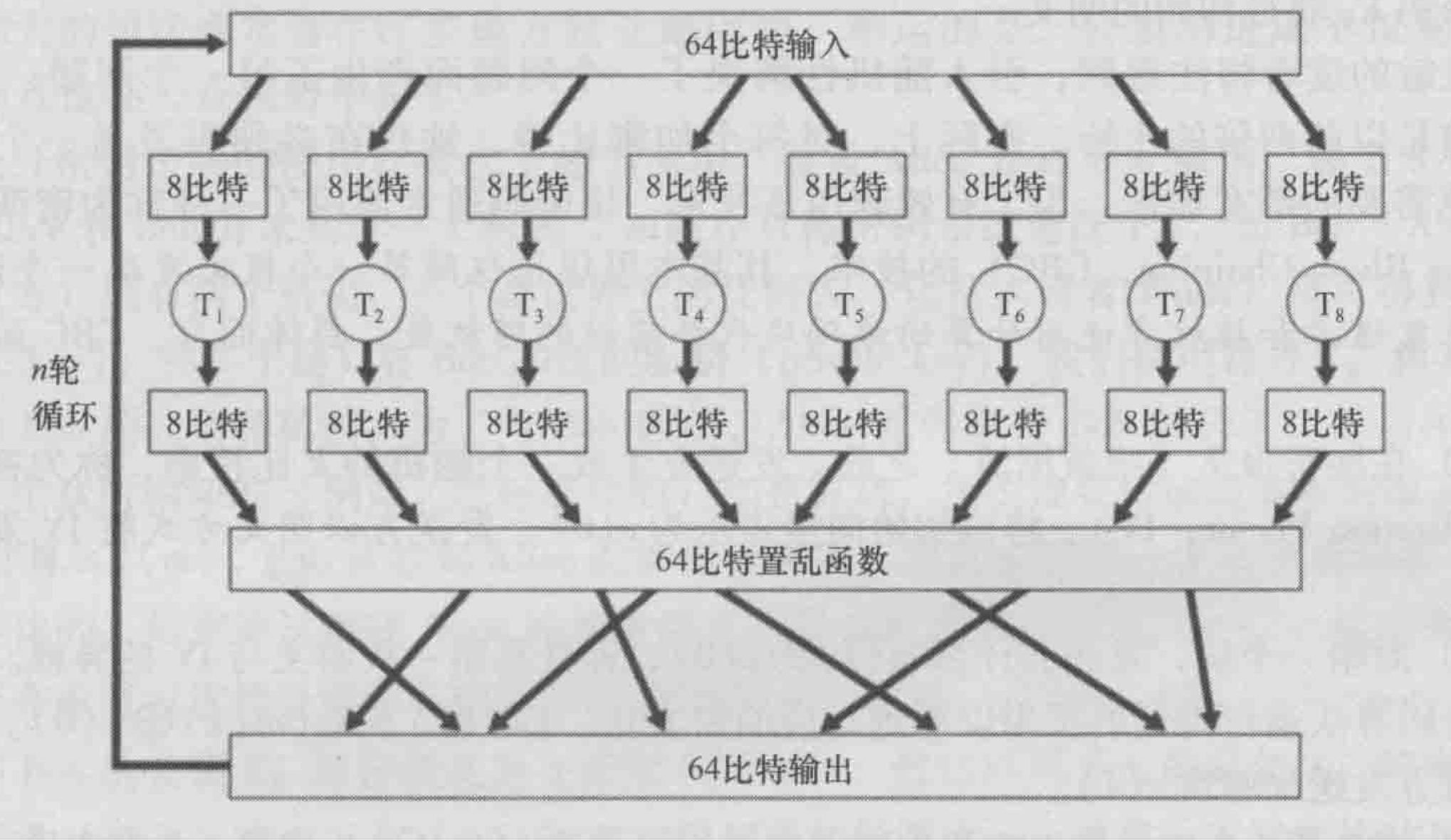 函数模拟随机排列表： * 64bit被划分成8个8bit的段，每个段由映射表处理。 * 8个输出重新装配成一个64bit块，作为输入块。 * 重复n次，循环的目的是让每个输入比特影响输出的大部分而不是全部。  #### 密码块链接 问题：对于相同的块，块密码将产生相同的密文。 方案：引入随机性。 问题：传输数据量增长。 密码块链接记录（Cipher Block Chaining，CBC）：仅随第一个报文发送一个随机值，然后使用计算的编码块代替后继的随机表。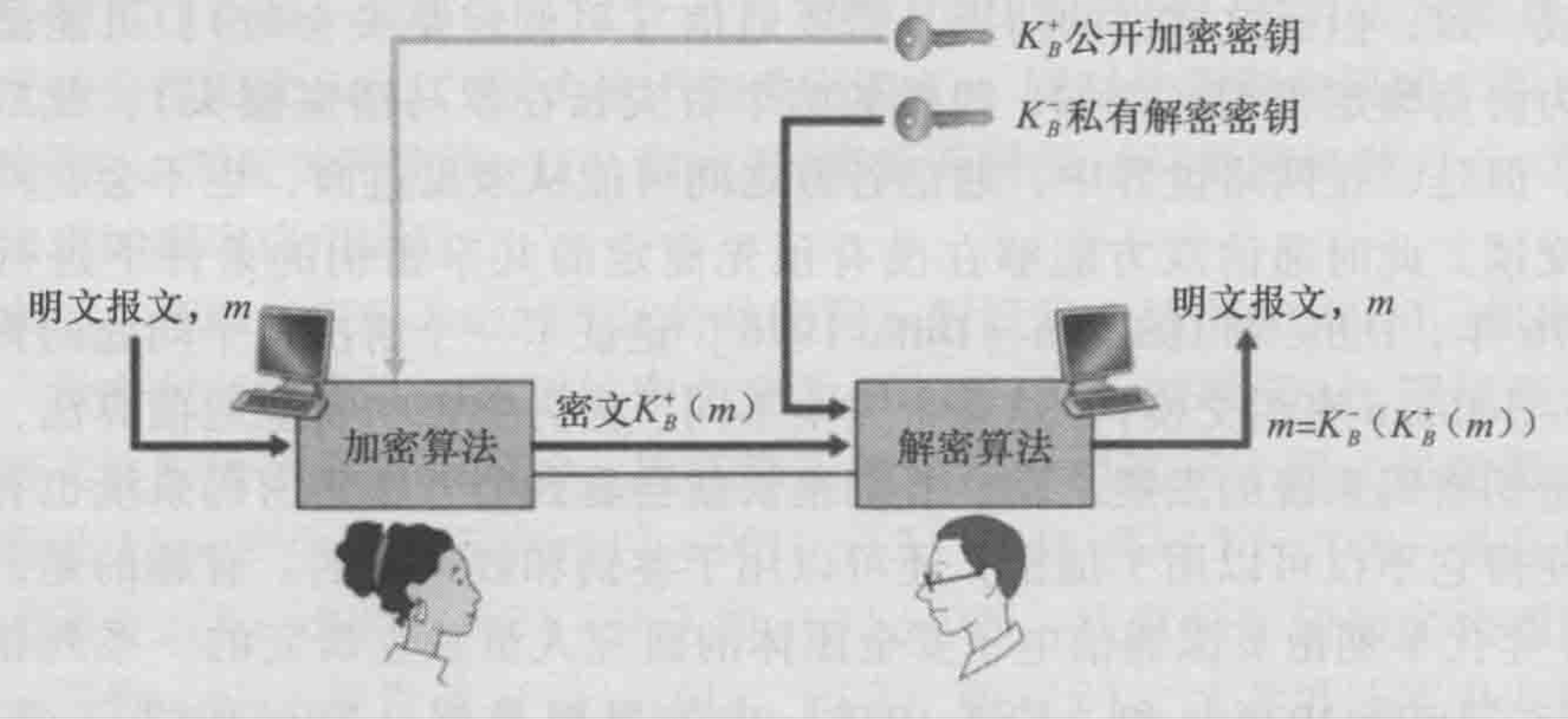 ### 8.2.2 公开密钥加密 发送方： * 获取接收方的公钥（Public Key），`$ K^{+} $`。 * 通过公钥和公开加密算法加密明文，`$ K^{+}(m) $`。 接收方：通过私钥和公开解密算法解密密文，`$ K^{-}(K^{+}(m)) $`。  #### RSA算法（RSA Algorithm） **生成公钥和私钥**： * 选择两个大素数p和q（p和q越大，破解RSA越困难，执行解密和加密的时间就越大）。 * 令 `$ n = pq $`，`$ z = (p-1)(q-1) $`。 * 选择一个小于 n 的数 e，且 e 与 z 互质。 * 求一个数 d，使得 `$ ed \mod z = 1 $`。 * 公钥 `$ K^{+}= (n, e) $`，私钥 `$ K^{-}=(n,d) $`。 **加密和解密算法**： * `$ K^{+}(m)=c=m^e \mod n $`。 * `$ K^{-}(c) = c^d \mod n $`。 #### 会话密钥 RSA要求的指数计算相对耗时，所以一般RSA与对称加密结合使用，通过RSA传递对称加密的密钥 `$ K_s $`。 #### RSA工作原理 z 为 n 的最小循环节。