# 三、小世界图
> 原文:[Chapter 3 Small world graphs](http://greenteapress.com/complexity2/html/thinkcomplexity2004.html)
> 译者:[飞龙](https://github.com/wizardforcel)
> 协议:[CC BY-NC-SA 4.0](http://creativecommons.org/licenses/by-nc-sa/4.0/)
> 自豪地采用[谷歌翻译](https://translate.google.cn/)
现实世界中的许多网络,包括社交网络在内,具有“小世界属性”,即节点之间的平均距离,以最短路径上的边数来衡量,远远小于预期。
在本章中,我介绍了斯坦利·米拉格(Stanley Milgram)的著名的“小世界实验”,这是小世界属性在真正的社交网络中的第一次科学演示。之后我们将考虑 Watts-Strogatz 图,它是一个小世界图的模型。我将复制 Watts 和 Strogatz 所做的实验,并解释它打算展示的东西。
这个过程中,我们将看到两种新的图算法:广度优先搜索(BFS)和 Dijkstra 算法,用于计算图中节点之间的最短路径。
本章的代码在本书仓库的`chap03.ipynb`中。使用代码的更多信息请参见第(?)章。
## 3.1 Stanley Milgram
斯坦利·米拉格(Stanley Milgram)是美国社会心理学家,他进行了两项最著名的社会科学实验,即 Milgram 实验,研究人们对权威的服从(<http://en.wikipedia.org/wiki/Milgram_experiment>)和小世界实验,研究了社交网络的结构(<http://en.wikipedia.org/wiki/Small_world_phenomenon>)。
在小世界实验中,Milgram 向堪萨斯州威奇托(Wichita, Kansas)的几个随机选择的人发送了包裹,带有一个指示,要求他们向马萨诸塞州沙龙(Sharon, Massachusetts)的目标人员发送一封附带的信(在我长大的地方,波士顿附近),目标人员通过名字和职业确定。受访者被告知,只有当他亲自认识目标人员时,才可以将该信直接邮寄给目标;否则他们按照指示,将信和同一个指示发送给他们认为的,更有可能认识目标人员的亲戚或朋友。
许多信件从来没有发出过,但是对于发出的信件,平均路径长度(信件转发次数)的大约为 6。这个结果用于确认以前的观察(和猜测),社交网络中任何两个人之间的通常距离是“六度分隔”。
这个结论令人惊讶,因为大多数人都希望社交网络本地化 - 人们往往会靠近他们的朋友 - 而且在一个具有本地连接的图中,路径长度往往会与地理距离成比例增加。例如,我的大多数朋友都住在附近,所以我猜想社交网络中节点之间的平均距离是大约 50 英里。威奇托距离波士顿约有 1600 英里,所以如果 Milgram 的信件穿过了社交网络的典型环节,那么他们应该有 32 跳,而不是 6 跳。
## 3.2 Watts 和 Strogatz
1998年,Duncan Watts 和 Steven Strogatz 在 Nature 杂志上发表了一篇“小世界网络的集体动态”(Collective dynamics of ’small-world’ networks)论文,提出了小世界现象的解释。 你可以从 <http://www.nature.com/nature/journal/v393/n6684/abs/393440a0.html> 下载。
Watts 和 Strogatz 从两种很好理解的图开始:随机图和正则图。在随机图中,节点随机连接。在正则图中,每个节点具有相同数量的邻居。他们考虑这些图的两个属性,群聚性和路径长度:
群聚是图表的“集团性”(cliquishness)的度量。在图中,集团是所有节点的子集,它们彼此连接;在一个社交网络中,集团是一群人,彼此都是朋友。Watts 和 Strogatz 定义了一个群聚系数,用于量化两个节点彼此连接,并同时连接到同一个节点的可能性。
路径长度是两个节点之间的平均距离的度量,对应于社交网络中的分离度。
Watts 和 Strogatz 表明,正则图具有高群聚性和长路径长度,而大小相同的随机图通常具有群聚性和短路径长度。所以这些都不是一个很好的社交网络模型,它是高群聚性与短路径长度的组合。
他们的目标是创造一个社交网络的生成模型。生成模型通过为构建或导致现象的过程建模,试图解释现象。Watts 和 Strogatz 提出了用于构建小世界图的过程:
1. 从一个正则图开始,节点为`n`,每个节点连接`k`个邻居。
2. 选择边的子集,并将它们替换为随机的边来“重新布线”。
边的重新布线的概率是参数`p`,它控制图的随机性。当`p = 0`时,该图是正则的;`p = 1`是随机的。
Watts 和 Strogatz 发现,较小的`p`值产生高群聚性的图,如正则图,短路径长度的图,如随机图。
在本章中,我将按以下步骤复制 Watts 和 Strogatz 实验:
+ 我们将从构建一个环格(ring lattice)开始,这是一种正则图。
+ 然后我们和 Watts 和 Strogatz 一样重新布线。
+ 我们将编写一个函数来测量群聚度,并使用 NetworkX 函数来计算路径长度。
+ 然后,我们为范围内的`p`值计算群聚度和路径长度。
+ 最后,我将介绍一种用于计算最短路径的高效算法,Dijkstra 算法。
## 3.3 环格
> 图 3.1 `n=10`,`k=4`的环格
正则图是每个节点具有相同数量的邻居的图;邻居的数量也称为节点的度。
环格是一种正则图,Watts 和 Strogatz 将其用作模型的基础。 在具有`n`个节点的环格中,节点可以排列成圆形,每个节点连接`k`个最近邻居。
例如,`n = 3`和`k = 2`的环形网格将拥有以下边:`(0, 1), (1, 2), (2, 0)`。 请注意,边从编号最高的节点“绕回”0。
更一般地,我们可以像这样枚举边:
```py
def adjacent_edges(nodes, halfk):
n = len(nodes)
for i, u in enumerate(nodes):
for j in range(i+1, i+halfk+1):
v = nodes[j % n]
yield u, v
```
`adjacent_edges`接受节点列表和参数`halfk`,它是`k`的一半。它是一个生成器函数,一次产生一个边。它使用模运算符`%`,从编号最高的节点绕回最低的节点。
我们可以这样测试:
```py
>>> nodes = range(3)
>>> for edge in adjacent_edges(nodes, 1):
... print(edge)
(0, 1)
(1, 2)
(2, 0)
```
现在我们可以使用`adjacent_edges`来生成环格。
```py
def make_ring_lattice(n, k):
G = nx.Graph()
nodes = range(n)
G.add_nodes_from(nodes)
G.add_edges_from(adjacent_edges(nodes, k//2))
return G
```
注意,`make_ring_lattice`使用地板除计算`halfk`,所以如果`k`是奇数,它将向下取整并产生具有度`k-1`的环格。这可能不是我们想要的,但现在还不错。
我们可以像这样测试函数:
```py
lattice = make_ring_lattice(10, 4)
```
图(?)展示了结果。
## 3.4 WS 图
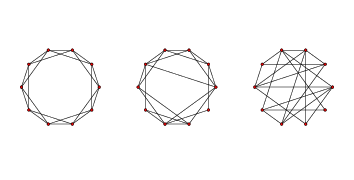
> 图 3.2 WS 图,`n=20`,`k=4`,`p=0`(左边),`p=0.2`(中间),`p=1`(右边)。
为了制作 Watts-Strogatz(WS)图,我们从一个环格开始,并为一些边“重新布线”。 在他们的论文中,Watts 和 Strogatz 以特定顺序考虑边,并用概率`p`重新布置每个边。 如果边被重新布置,则它们使第一个节点保持不变,并随机选择第二个节点。它们不允许自环或多边;也就是说,节点不能拥有到它自身的边,并且两个节点之间不能拥有多个边。
这是我的这个过程的实现。
```py
def rewire(G, p):
nodes = set(G.nodes())
for edge in G.edges():
if flip(p):
u, v = edge
choices = nodes - {u} - set(G[u])
new_v = choice(tuple(choices))
G.remove_edge(u, v)
G.add_edge(u, new_v)
```
参数`p`是边的重新布线的概率。`for`循环枚举了边,并使用`flip`,它以概率`p`返回`True`,来选择哪些被重新布置。
如果我们重新布置节点`u`到节点`v`的边,我们必须选择一个节点来替换`v`,称为`new_v`。为了计算可能的选择,我们从节点集开始,它是一个集合,并且移除`u`和它的邻居,这避免了自环和多边。
然后我们从选项中选择new_v,将`u`到`v`的现有删除,并从添加一个`u`到`new_v`的新边。
另外,表达式`G[u]`返回一个字典,他的键是包含`u`的邻居。在这种情况下,它比使用`G.neighbors`更快一点。
这个函数不按照 Watts 和 Strogatz 指定的顺序考虑边缘,但它似乎不会影响结果。
图(?)展示了`n = 20`,`k = 4`和范围内`p`值的 WS 图。当`p = 0`时,该图是环格。 当`p = 1`时,它是完全随机的。我们将看到,有趣的事情发生在两者之间。
## 3.5 群聚性
下一步是计算群聚系数,它量化了节点形成集团的趋势。 集团是一组完全连接的节点;也就是说,在集团中的所有节点对之间都存在边。
假设一个特定的节点`u`具有`k`个邻居。如果所有的邻居都相互连接,则会有`k(k-1)/2`个边。 实际存在的这些边的比例是`u`的局部群聚系数,表示为`Cu`。它被称为“系数”,因为它总是在 0 和 1 之间。
如果我们计算所有节点上的`Cu`平均值,我们得到“网络平均群聚系数”,表示为`C`。
这是一个计算它的函数。
```py
def node_clustering(G, u):
neighbors = G[u]
k = len(neighbors)
if k < 2:
return 0
total = k * (k-1) / 2
exist = 0
for v, w in all_pairs(neighbors):
if G.has_edge(v, w):
exist +=1
return exist / total
```
同样,我使用`G [u]`,它返回一个字典,键是节点的邻居。如果节点的邻居少于两个,则群聚系数未定义,但为简便起见,`node_clustering`返回 0。
否则,我们计算邻居之间的可能的边数量,`total`,然后计算实际存在的边数量。结果是存在的所有边的比例。
我们可以这样测试函数:
```py
>>> lattice = make_ring_lattice(10, 4)
>>> node_clustering(lattice, 1)
0.5
```
在`k=4`的环格中,每个节点的群聚系数是`0.5`(如果你不相信,可以看看图(?))。
现在我们可以像这样计算网络平均群聚系数:
```py
def clustering_coefficient(G):
cc = np.mean([node_clustering(G, node) for node in G])
return cc
```
`np.mean` 是个 NumPy 函数,计算列表或数组中元素的均值。
然后我们可以像这样测试:
```py
>>> clustering_coefficient(lattice)
0.5
```
这个图中,所有节点的局部群聚系数是 0.5,所以节点的平均值是 0.5。当然,我们期望这个值和 WS 图不同。
## 3.6 最短路径长度
下一步是计算特征路径长度`L`,它是每对节点之间最短路径的平均长度。 为了计算它,我将从 NetworkX 提供的函数开始,`shortest_path_length`。 我会用它来复制 Watts 和 Strogatz 实验,然后我将解释它的工作原理。
这是一个函数,它接受图并返回最短路径长度列表,每对节点一个。
```py
def path_lengths(G):
length_map = nx.shortest_path_length(G)
lengths = [length_map[u][v] for u, v in all_pairs(G)]
return lengths
```
`nx.shortest_path_length`的返回值是字典的字典。外层字典每个节点`u`到内层字典的映射,内层字典是每个节点`v`到`u->v`的最短路径长度的映射。
使用来自`path_lengths`的长度列表,我们可以像这样计算`L`:
```py
def characteristic_path_length(G):
return np.mean(path_lengths(G))
```
并且我们可以使用小型的环格来测试它。
```py
>>> lattice = make_ring_lattice(3, 2)
>>> characteristic_path_length(lattice)
1.0
```
这个例子中,所有三个节点都互相连接,所以平均长度为 1。
## 3.7 WS 实验
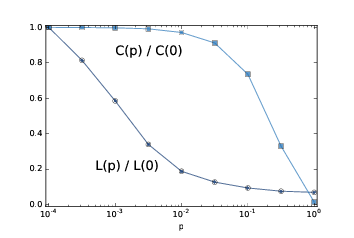
> 图 3.3:WS 图的群聚系数`C`和特征路径长度`L`,其中`n=1000, k=10`,`p`是一个范围。
现在我们准备复制 WS 实验,它表明对于一系列`p`值,WS 图具有像正则图像那样的高群聚性,像随机图一样的短路径长度。
我将从`run_one_graph`开始,它接受`n`,`k`和`p`;它生成具有给定参数的 WS图,并计算平均路径长度`mpl`和群聚系数`cc`:
```py
def run_one_graph(n, k, p):
ws = make_ws_graph(n, k, p)
mpl = characteristic_path_length(ws)
cc = clustering_coefficient(ws)
print(mpl, cc)
return mpl, cc
```
Watts 和 Strogatz 用`n = 1000`和`k = 10`进行实验。使用这些参数,`run_one_graph`在我的电脑上需要大约一秒钟;大部分时间用于计算平均路径长度。
现在我们需要为范围内的`p`计算这些值。我将再次使用 NumPy 函数`logspace`来计算`ps`:
```py
ps = np.logspace(-4, 0, 9)
```
对于每个`p`的值,我生成了 3 个随机图,并且我们将结果平均。这里是运行实验的函数:
```py
def run_experiment(ps, n=1000, k=10, iters=3):
res = {}
for p in ps:
print(p)
res[p] = []
for _ in range(iters):
res[p].append(run_one_graph(n, k, p))
return res
```
结果是个字典,将每个`p`值映射为`(mpl, cc)`偶对的列表。
最后一步就是聚合结果:
```py
L = []
C = []
for p, t in sorted(res.items()):
mpls, ccs = zip(*t)
mpl = np.mean(mpls)
cc = np.mean(ccs)
L.append(mpl)
C.append(cc)
```
每次循环时,我们取得一个`p`值和一个`(mpl, cc)`偶对的列表。 我们使用`zip`来提取两个列表,`mpls`和`ccs`,然后计算它们的均值并将它们添加到`L`和`C`,这是路径长度和群聚系数的列表。
为了在相同的轴上绘制`L`和`C`,我们通过除以第一个元素,将它们标准化:
```py
L = np.array(L) / L[0]
C = np.array(C) / C[0]
```
图(?)展示了结果。 随着`p`的增加,平均路径长度迅速下降,因为即使少量随机重新布线的边,也提供了图区域之间的捷径,它们在格中相距很远。另一方面,删除局部链接降低了群聚系数,但是要慢得多。
因此,存在较宽范围的`p`,其中 WS 图具有小世界图的性质,高群聚度和短路径长度。
这就是为什么 Watts 和 Strogatz 提出了 WS 图,作为展示小世界现象的,现实世界网络的模型。
## 3.8 能有什么解释?
如果你问我,为什么行星轨道是椭圆形的,我最开始会为一个行星和一个恒星建模;我将在 <http://en.wikipedia.org/wiki/Newton's_law_of_universal_gravitation> 上查找万有引力定律,并用它为行星的运动写出一个微分方程。之后我会扩展轨道方程式,或者更有可能在 <http://en.wikipedia.org/wiki/Orbit_equation> 上查找。通过一个小的代数运算,我可以得出产生椭圆轨道的条件。之后我会证明我们看做行星的物体满足这些条件。
人们,或至少是科学家,一般对这种解释感到满意。它有吸引力的原因之一是,模型中的假设和近似值似乎是合理的。行星和恒星不是真正的质点,但它们之间的距离是如此之大,以至于它们的实际尺寸可以忽略不计。同一太阳系中的行星可以影响彼此的轨道,但效果通常较小。而且我们忽视相对论的影响,再次假定它们很小。
这也因为它是基于方程式的。我们可以用闭式表达轨道方程,这意味着我们可以有效地计算轨道。这也意味着我们可以得出轨道速度,轨道周期和其他数量的一般表达式。
最后,我认为这是因为它具有数学证明的形式。它从一组公理开始,通过逻辑和分析得出结果。但重要的是要记住,证明属于模型,而不是现实世界。也就是说,我们可以证明,行星的理想模型产生一个椭圆轨道,但是我们不能证明这个模型与实际的行星有关(实际上它不是)。
+ 这些模型可以做什么工作:它们是预测性的还是说明性的,还是都有?
+ 这些模型的解释,是否比基于更传统模型的解释更不满意?为什么?
+ 我们应该如何刻画这些和更传统的模型之间的差异?他们在种类还是程度上不同?
在这本书中,我将提供我对这些问题的回答,但它们是暂时性的,有时是投机性的。我鼓励你怀疑地思考他们,并得出你自己的结论。
## 3.9 广度优先搜索
当我们计算最短路径时,我们使用了 NetworkX 提供的一个函数,但是我没有解释它是如何工作的。为此,我将从广度优先搜索开始,这是用于计算最短路径的 Dijkstra 算法的基础。
在第(?)节,我提出了`reachable_nodes`,它寻找从给定的起始节点可以到达的所有节点:
```py
def reachable_nodes(G, start):
seen = set()
stack = [start]
while stack:
node = stack.pop()
if node not in seen:
seen.add(node)
stack.extend(G.neighbors(node))
return seen
```
我当时没有这么说,但它执行深度优先搜索(DFS)。现在我们将修改它来执行广度优先搜索(BFS)。
为了了解区别,想象一下你正在探索一座城堡。你最开始在一个房间里,带有三个门,标记为 A,B 和 C 。你打开门 C 并发现另一个房间,它的门被标记为 D ,E 和 F。
下面你打开哪个门呢?如果你打算冒险,你可能想更深入城堡,选择 D,E 或 F。这是一个深度优先搜索。
但是,如果你想更系统化,你可以在 D,E 和 F 之前回去探索 A 和 B,这将是一个广度优先搜索。
在`reachable_nodes`中,我们使用`list.pop`选择下一个节点来“探索”。默认情况下,`pop`返回列表的最后一个元素,这是我们添加的最后一个元素。在这个例子中,这是门 F。
如果我们要执行 BFS,最简单的解决方案是将第一个元素从栈中弹出:
```py
node = stack.pop(0)
```
这有效,但速度很慢。在 Python 中,弹出列表的最后一个元素需要常数时间,但是弹出第一个元素线性于列表的长度。在最坏的情况下,就是堆栈的长度`O(n)`,这使得 BFS 的`O(nm)`的实现比`O(n + m)`差得多。
我们可以用双向队列(也称为`deque`)来解决这个问题。`deque`的一个重要特征就是,你可以在开头和末尾添加和删除元素。要了解如何实现,请参阅 <https://en.wikipedia.org/wiki/Double-ended_queue>。
Python 在`collections`模块中提供了`deque`,所以我们可以像这样导入它:
```py
from collections import deque
```
我们可以使用它来编写高效的 BFS:
```py
def reachable_nodes_bfs(G, start):
seen = set()
queue = deque([start])
while queue:
node = queue.popleft()
if node not in seen:
seen.add(node)
queue.extend(G.neighbors(node))
return seen
```
差异在于:
+ 我用名为`queue`的`deque`替换了名为`stack`的列表。
+ 我用`popleft`替换`pop`,它删除并返回队列的最左边的元素,这是第一个添加的元素。
这个版本恢复为`O(n + m)`。现在我们做好了寻找最短路径的准备。
## 3.10 (简化的)Dijkstra 算法
Edsger W. Dijkstra 是荷兰计算机科学家,发明了一种有效的最短路径算法(参见 <http://en.wikipedia.org/wiki/Dijkstra's_algorithm>)。他还发明了信号量,它是一种数据结构,用于协调彼此通信的程序(参见 <http://en.wikipedia.org/wiki/Semaphore_(programming>)和 Downey,《The Little Book of Semaphores》)。
作为一系列计算机科学论文的作者,Dijkstra 是著名(臭名昭著)的。 有些比如“反对 GOTO 语句的案例”(A Case against the GO TO Statement),对编程实践产生了深远的影响。其他比如“真正的计算机科学教学的残酷”(On the Cruelty of Really Teaching Computing Science),很有娱乐性,但效果却不好。
Dijkstra 算法解决了“单源最短路径问题”,这意味着它寻找从给定的“源”节点到图中每个其他节点(或至少每个连接节点)的最小距离。
我们最开始考虑算法的简化版本,所有边的长度相同。更一般的版本适用于任何非负的边的长度。
简化版本类似于第一节中的广度优先搜索 除了我们用称为`dist`的字典替换集合`seen`,该字典将每个节点映射为与源的距离:
```py
def shortest_path_dijkstra(G, start):
dist = {start: 0}
queue = deque([start])
while queue:
node = queue.popleft()
new_dist = dist[node] + 1
neighbors = set(G[node]) - set(dist)
for n in neighbors:
dist[n] = new_dist
queue.extend(neighbors)
return dist
```
这是它的工作原理:
+ 最初,队列包含单个元素`start`,`dist`将`start`映射为距离 0(这是`start`到自身的距离)。
+ 每次循环中,我们使用`popleft`获取节点,按照添加到队列的顺序。
+ 接下来,我们发现节点的所有邻居都没有在`dist`中。
+ 由于从起点到节点的距离是`dist [node]`,到任何未访问的邻居的距离是`dist [node] +1`。
+ 对于每个邻居,我们向`dist`添加一个条目,然后将邻居添加到队列中。
只有在我们使用 BFS 而不是 DFS 时,这个算法才有效。为什么?
第一次循环中,`node`是`start`,`new_dist`为`1`。所以`start`的邻居距离为 1,并且进入了队列。
当我们处理`start`的邻居时,他们的所有邻居距离为`2`。我们知道,他们中没有一个距离为`1`,因为如果有的话,我们会在第一次迭代中发现它们。
类似地,当我们处理距离为 2 的节点时,我们将他们的邻居的距离设为`3`。我们知道它们中没有一个的距离为`1`或`2`,因为如果有的话,我们将在之前的迭代中发现它们。
等等。如果你熟悉归纳证明,你可以看到这是怎么回事。
但是,在我们开始处理距离为`2`的节点之前,只有我们处理了距离为`1`的所有节点,这个论证才有效,依此类推。这正是 BFS 所做的。
在本章末尾的练习中,你将使用 DFS 编写 Dijkstra 算法的一个版本,以便你有机会看到出现什么问题。
## 3.11 练习
练习 1:
在一个环格中,每个节点的邻居数量相同。邻居的数量称为节点的度,所有节点的度相同的图称为正则图。
所有环格都是正则的,但不是所有的正则图都是环格。特别地,如果`k`是奇数,则不能构造环格,但是我们可以构建一个正则图。
编写一个名为`make_regular_graph`的函数,该函数接受`n`和`k`,并返回包含`n`个节点的正则图,其中每个节点都有`k`个邻居。如果不可能使用`n`和`k`的给定值来制作正则图,则该函数应该抛出`ValueError`。
练习 2:
我的`reachable_nodes_bfs`实现是有效的,因为它是`O(n + m)`的,但它产生了很多开销,将节点添加到队列中并将其删除。 NetworkX 提供了一个简单,快速的 BFS 实现,可从 GitHub 上的 NetworkX 仓库获取,网址为 <https://github.com/networkx/networkx/blob/master/networkx/algorithms/components/connected.py>。
这里是我修改的一个版本,返回一组节点:
```py
def _plain_bfs(G, source):
seen = set()
nextlevel = {source}
while nextlevel:
thislevel = nextlevel
nextlevel = set()
for v in thislevel:
if v not in seen:
seen.add(v)
nextlevel.update(G[v])
return seen
```
将这个函数与`reachable_nodes_bfs`相比,看看哪个更快。之后看看你是否可以修改这个函数来实现更快的`shortest_path_dijkstra`版本。
练习 3:
下面的 BFS 实现包含两个性能错误。它们是什么?这个算法的实际增长级别是什么?
```py
def bfs(top_node, visit):
"""Breadth-first search on a graph, starting at top_node."""
visited = set()
queue = [top_node]
while len(queue):
curr_node = queue.pop(0) # Dequeue
visit(curr_node) # Visit the node
visited.add(curr_node)
# Enqueue non-visited and non-enqueued children
queue.extend(c for c in curr_node.children
if c not in visited and c not in queue)
```
练习 4:在第(?)节中,我说了除非使用 BFS,Dijkstra 算法不能工作。编写一个`shortest_path_dijkstra `的版本,它使用 DFS,并使用一些例子测试它,看看哪里不对。
练习 5:
Watts 和 Strogatz 的论文的一个自然问题是,小世界现象是否特定于它的生成模型,或者其他类似模型是否产生相同的定性结果(高群聚和短路径长度)。
为了回答这个问题,选择 WS 模型的一个变体并重复实验。 你可能会考虑两种变体:
+ 不从常规图开始,从另一个高群聚的图开始。 例如,你可以将节点放置在二维空间中的随机位置,并将每个节点连接到其最近的`k`个邻居。
+ 尝试不同种类的重新布线。
如果一系列类似的模型产生类似的行为,我们认为论文的结果是可靠的。
练习 6:
Dijkstra 算法解决了“单源最短路径”问题,但为了计算图的特征路径长度,我们其实需要解决“多源最短路径”问题。
当然,一个选择是运行 Dijkstra 算法`n`次,每个起始节点一次。 对于某些应用,这可能够好,但是有更有效的替代方案。
找到一个多源最短路径的算法并实现它。请参阅 <https://en.wikipedia.org/wiki/Shortest_path_problem#All-pairs_shortest_paths>。
将实现的运行时间与运行 Dijkstra 算法`n`次进行比较。哪种算法在理论上更好?哪个在实践中更好?NetworkX 使用了哪一个?
